Образовака📐 Геометрия10 классМногогранники

Диагональ прямоугольного параллелепипеда

4.6

Средняя оценка: 4.6

Всего получено оценок: 103.

В геометрии 10 класса есть разделы, изучающие свойства диагонали прямоугольного параллелепипеда. Свойства изучаются не просто так, много задач на нахождение диагонали этой фигуры встречаются в ЕГЭ. Поэтому имеет смысл подробно поговорить о характеристиках диагонали прямоугольного параллелепипеда.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Определение понятия

В общем случае диагональ представляет собой отрезок, соединяющий вершины двух углов, не принадлежащих одной стороне многогранника. Прямоугольный параллелепипед в свою очередь состоит из шести граней, являющихся прямоугольниками.

Диагонали в прямоугольном параллелепипеде могут быть проведены не только во внутреннем пространстве фигуры, но и на боковых гранях, и в гранях оснований. В последнем случае обычно уточняется, что речь идет о диагонали боковой грани или диагонали основания.

Диагональ параллелепипеда — Рис. 1. Диагонали параллелепипеда.

У параллелепипеда есть четыре диагонали. Причем, эти отрезки не принадлежат ни одной боковой грани или основаниям, а проводятся внутри фигуры.

Характеристики диагонали

Существует две теоремы, касающиеся диагоналей параллелограмма. Чтобы их доказать, используются дополнительные построения. К примеру, часто диагональ нижнего основания данной объемной геометрической фигуры служит стороной для нескольких треугольников.

Первая Теорема

Квадрат диагонали прямоугольного параллелепипеда можно найти, суммировав квадраты трех измерений этой геометрической фигуры.

Здесь речь идет о длине, ширине и высоте рассматриваемого многогранника. Чтобы доказать данную теорему необходимо использовать свойства прямоугольных треугольников.

Диагональ, проведенная в основании будет являться гипотенузой прямоугольного треугольника $АВС$, значит ее можно найти по теореме Пифагора через сумму квадратов $АВ$ и $ВС$.

Но $АВ$ и $ВС$ это длина и ширина параллелепипеда.

$$АC=\sqrt{AB^2+BC^2}$$

Затем рассмотрим прямоугольный треугольник $АСС’$. Диагональ $АС’$ также можно найти через теорему Пифагора, как корень из суммы катетов $АС$ и $СС’$. Но $АС$ мы уже находили как корень из суммы квадратов $АВ$ и $АС$:

$(ACʹ)^2= (CCʹ)^2+(CD)^2+(CB)^2$, где

$CCʹ$ – высота;

$CD$ – длина;

$CB$ – ширина.

Так выглядит формула, отражающая содержание данной теоремы.

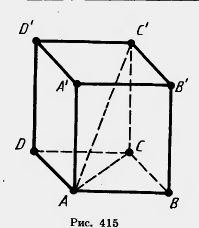
Рис. 2. Связь диагонали параллелепипеда с ребром и основанием.

Обычно больший отрезок, лежащий в основании параллелепипеда, считается ее длиной. Меньший отрезок – шириной.

Вторая теорема

В любом параллелепипеде четыре диагонали пересекаются в одной точке, которую называют точкой симметрии, и делятся ею пополам. Это свойство доказывают, рассматривая две любые диагонали, и проводя соответствующие отрезки.

Для доказательства этой теоремы нужно вспомнить, что плоскость может задаваться двумя пересекающимися прямыми. В рассматриваемом случае, сечение плоскостью, заданной двумя пересекающимися диагоналями, принимает форму прямоугольника. А диагонали прямоугольника, как известно, точкой пересечения делятся пополам.

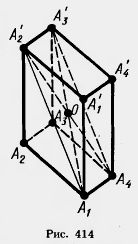
Рис. 3. Пересечение диагоналей параллелепипеда.

Из этой же теоремы можно сделать вывод о том, что все его диагонали будут равными между собой отрезками.

Что мы узнали?

Мы поговорили о диагоналях прямоугольного параллелепипеда. Узнали, что, используя свойства диагоналей параллелепипеда, можно найти ширину, длину и высоту параллелепипеда. Поговорили о том, как найти центр симметрии, и определить длину диагоналей прямоугольного параллелепипеда.