Перевод систем счисления
В решении определенного класса задач иногда удобно записывать числовые значения в разных системах счисления. Разработан ряд унифицированных правил перевода чисел между системами. О том, как выполняется перевод систем счисления, рассказано в статье.
Что такое перевод систем счисления
Основанием системы счисления является величина, определяющая количество символов для записи числового значения. Например, основанием двоичной системы является число 2, пятеричной, соответственно – 5.
Число 15 в десятичной системе при переводе в пятеричную равно 30, а в восьмеричной будет равно 17. Шестнадцатеричный эквивалент пятнадцати представляет собой букву F. Как так получается?
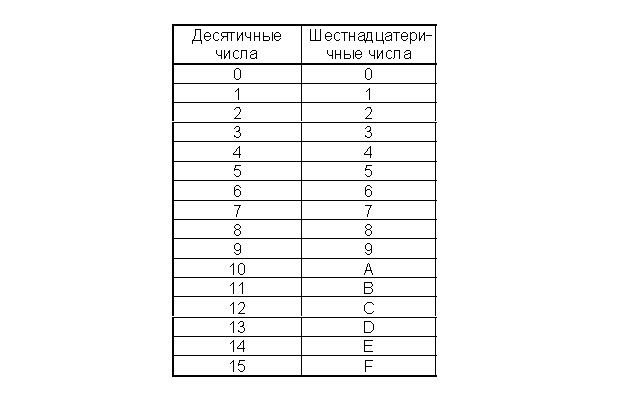
Перевод чисел с участием десятичной системы счисления
В преобразовании чисел с участием десятичной системы приняты три строгих правила перевода.
1. Пересчет числового значения из десятичного формата в эквивалент другой системы счисления заключается в делении целой части и полученных частных, на величину основания будущей системы счисления. При этом остатки от деления записываются начиная с последнего.
Например, 15 из десятичной системы в восьмеричную переводится так: 15 / 8 = 1 (в остатке 7). Записываем итог, начиная с конечного и в данном случае единственного частного, и затем остаток. Получим 17.
Еще один пример: десятичное 125 в восьмеричной системе: 125 / 8 = 15 (5). Полученное частное больше, чем основание 8.
Продолжаем делить: 15 / 8 = 1 (7). Ответ записывается с последнего частного, а затем остатки от деления: 175.
Следует запомнить, что запись результата всегда начинает с последнего частного и остатков от деления в обратном порядке.
2. Преобразование части десятичного числа, записанной после запятой, выполняется с помощью обратной процедуры, то есть умножения, вычисляя одно за другим произведения дробных частей на основание будущей системы счисления и записывая последовательно цифры, полученные в целой части. Например, дробная часть числа 0,134 в двоичную систему переводится так (удобнее это делать столбиком):
0,134 * 2 = 0,268 (в целой части 0)
0,268 * 2 = 0,536 (0)
0,536 * 2 = 1,072 (слева от запятой 1)
0,072 * 2 = 0,144 (в целой части 0)
0,144 * 2 = 0,288 (0)
Произведения вычисляют до тех пор, пока не будет обеспечена заданная точность или в остатке не получится ноль.
Ответ: десятичное 0,134 в двоичной системе равно 0,00100.
При умножении следует брать только остатки, не учитывая полученную цифру в целой части.
3. Перевод чисел из разных систем счисления в десятичную удобнее всего представлять с помощью развернутой записи числа, или при использовании формулы полинома, который формируется путем сложения одночленов, возведенных в степень и умноженных на некоторые коэффициенты:
a1 * x^(n-1) + a2 * x^(n-2) + a3 * x^(n-3) + …+an * x^0
Например, 137 = 1 * 10^2 + 3 * 10^1 + 7 * 10^0.
Рассмотрим примеры перевода чисел:
2 →10: 11011 = 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 27
8 →10: 134 = 1 * 8^2 + 3 * 8^1 + 4 * 8^0 = 92
16 → 10: 1AF = 1 * 16^2 + 10 * 16^1 + 15 * 16^0 = 431
Перевод чисел в системах счислении, построенных на бинарном основании
Восьмеричная и шестнадцатеричные системы счисления построены на бинарном базисе. Основанием восьмеричной системы является число 8, то есть 2^3, а основание шестнадцатеричной системы 16 = 2^4. Перевод между этими системами и двоичной системой удобнее всего выполнять с помощью таблицы перевода систем счисления:
Каждое восьмеричное число представляется триадой (тремя элементами) двоичных знаков, каждое шестнадцатеричное – двоичной тетрадой (четыре элемента).
Например, 8 → 2: 134 ⇔ 001011100
16 → 2: 8F ⇔ 10001111
2 → 8: 110101 ⇔ 65
2 → 16: 11011000 ⇔ D8
Что мы узнали?
Переход между различными системами счисления выполняется по строго определенным правилам. Десятичные числа преобразуются в другие системы путем последовательного деления целой части и умножения дробной, обратный перевод выполняется с помощью полинома. Перевод между 2-, 8- и 16-ми системами выполняется по таблице.
