Площадь поверхности цилиндра

4.6

Средняя оценка: 4.6

Всего получено оценок: 9436.

4.6

Средняя оценка: 4.6

Всего получено оценок: 9436.

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

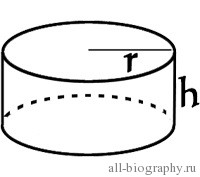У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.

Известно, что площадь окружности равна πr². Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr² + πr² = 2πr².

Боковая поверхность цилиндра

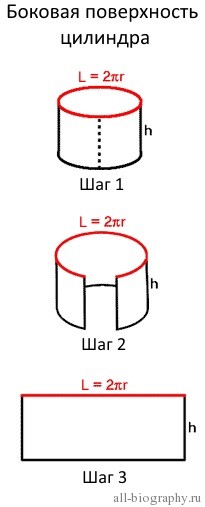Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Площадь полной поверхности цилиндра

Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr² + πr² + 2πrh = 2πr² + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Тест по теме

Доска почёта

Чтобы попасть сюда - пройдите тест.