Образовака🌡️ Физика8 классСветовые явления

Рассеивающая линза

4.8

Средняя оценка: 4.8

Всего получено оценок: 113.

Линза — это тело, способное пропускать свет, состоящее из двух поверхностей. Одна поверхность линзы сферическая, вторая может быть или сферической или плоской. Линза может быть собирающей или рассеивающей. Рассмотрим свойства рассеивающей линзы, дадим определение, приведём формулу рассеивающей линзы.

Ход лучей в линзе

Применение линз основано на их способности искривлять лучи света. Коэффициент преломления стекла отличается от коэффициента преломления воздуха, а поэтому луч, падающий на линзу, преломляется. При выходе из линзы происходит второе преломление.

Лучи, прошедшие сквозь линзу, будут либо отклоняться к оптической оси (такая линза называется собирающей), либо отклоняться в сторону от оптической оси (такая линза называется рассеивающей).

Способность отклонять лучи от прямолинейного распространения называется оптической силой линзы. Если у линзы большая оптическая сила, то у неё будет малое фокусное расстояние, и наоборот. Таким образом, оптическая сила линзы — это величина, обратная фокусному расстоянию. Она измеряется в диоптриях. Для рассеивающей линзы фокусное расстояние и оптическая сила отрицательны.

Рассеивающая линза

Если толщина линзы в центре меньше, чем по краям, — лучи, прошедшие сквозь такую линзу, будут отклоняться от оптической оси. Однако если продолжить линии хода лучей, то они сойдутся в фокальной плоскости перед линзой. То есть после рассеивающей линзы лучи, параллельные главной оптической оси, направлены так, что они как бы выходят из точки пересечения фокальной плоскости и оси. Такая точка называется фокусом рассеивающей линзы.

Фокус рассеивающей линзы — это чисто геометрический объект. В нём сходятся лишь продолжения лучей, реального «выхода лучей из фокуса» нет. Поэтому фокус рассеивающей линзы является мнимым.

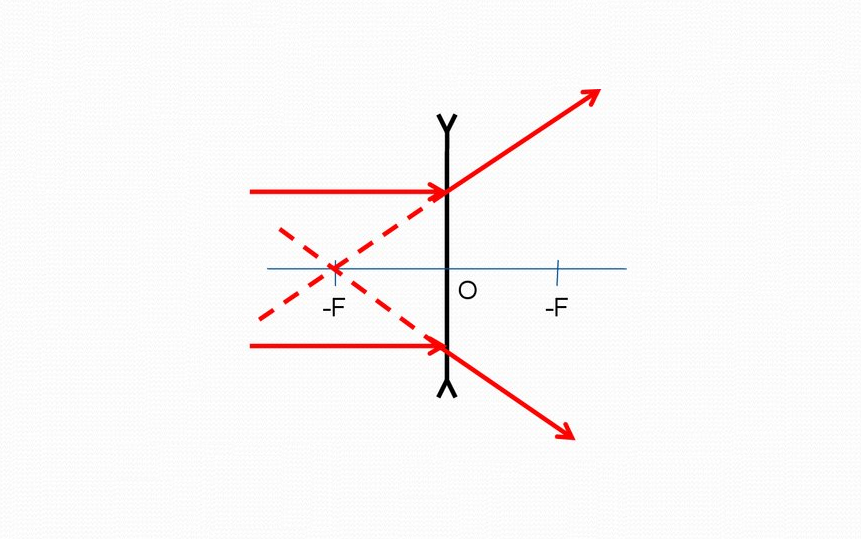
Изображение, даваемое рассеивающей линзой

Из курса физики в 8 классе известно: чтобы построить изображение точки, которое даёт рассеивающая линза, строится схема хода лучей. Из реальной точки «пускаются» два луча, в точке их пересечения будет изображение.

Лучи, прошедшие сквозь рассеивающую линзу, расходятся. Поэтому пересечения самих лучей после линзы не будет. Однако если продолжить линии хода лучей, то они пересекутся в точке перед линзой, создавая мнимое изображение.

Как правило, используются следующие два луча:

луч, проходящий через линзу без изменений: он проходит через оптический центр линзы;
луч, продолжение которого пройдёт через фокус линзы: он параллелен оптической оси.

После построения линий хода этих двух луче также потребуется достроить продолжение линий до их пересечения. Пересекутся они перед рассеивающей линзой, образуя мнимое изображение. Расстояние до этого изображения можно определить из формулы рассеивающей линзы:

$${1\over d}+{1\over f}=D$$

где:

$d$ — расстояние от точки до линзы;
$f$ — расстояние от линзы до изображения (отрицательное);
$D$ — оптическая сила линзы (отрицательная).

Рис. 3. Изображение, даваемое рассеивающей линзой.

Что мы узнали?

Линза — это прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина линзы в середине меньше, чем по краям, то лучи, прошедшие сквозь неё, расходятся, и эта линза называется рассеивающей. Фокус и изображение, построенные рассеивающей линзой, находятся перед ней и являются мнимыми.