Аксиома параллельных прямых


Средняя оценка: 4.2
Всего получено оценок: 213.
Средняя оценка: 4.2
Всего получено оценок: 213.
Аксиома параллельных прямых – это один из постулатов Евклидовой геометрии, на которой построено доказательство всех современных теорем стереометрии. Это определение не только математическое, но и историческое. Именно о формулировке, истории появления и интересном признаке, который следует из этих утверждений и пойдет речь сегодня.
Немного истории
Почти все современные источники приписывают формулировку аксиомы Евклиду, но на самом деле родоначальник геометрии сформулировал немного другую аксиому, а вернее даже не аксиому, а скорее признак. Что интересно, его долгое время пытались опровергнуть, но сегодня перестали.
Пятый постулат или аксиома Евклида звучит так: Если при пересечении двух прямых третьей, сумма односторонних углов менее 180 градусов, то такие прямые пересекаются, при том с той стороны, где сумма углов меньше 180.
Ничего не напоминает? Конечно же, это третий признак параллельности прямых, вывернутый наизнанку: две прямые параллельны, если односторонние углы в сумме дают 180 градусов.
А современная трактовка аксиомы: Через точку в плоскости может быть проведена одна и только одна прямая параллельная данной – принадлежит другому древнегреческому математику – Проклу. Вот такая небольшая историческая ошибка.
Формулировка
Но кто бы там ни был автором аксиомы, в любой задаче и при любом доказательстве, нужно иметь в виду: утверждение зовется аксиомой параллельных прямых и формулируется так: через точку на плоскости можно провести только одну прямую параллельную данной.
Следствия
Эта аксиома имеет два следствия, которые еще называют свойствами параллельных прямых.
На самом деле, следствий три, но третье в своем доказательстве имеет не только аксиому, а поэтому следствием в полной мере считаться не может. Формулируется третье следствие так: Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй. Мы докажем это утверждение чуть позже.
Первое следствие из аксиомы параллельных прямых звучит так: если прямая параллельна одной из параллельных прямых, то она параллельна и третьей.

Второе следствие: Если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
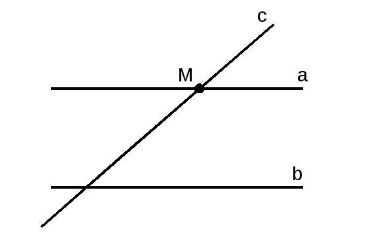
Оба следствия доказываются методом от противного.
Задача
Третье следствие всегда доказывается учениками как задача. Итак, необходимо доказать, что если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй.
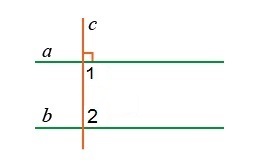
Проведем две параллельные прямые а и b. Прямая с перпендикулярна прямой а. Это значит, что прямая с пересекает прямую а, то есть по следствия 2 из аксиомы о параллельности прямых, прямая с пересечет и прямую b, так как b и а параллельны.
Обратим внимание на углы 1 и 2 – они являются односторонними при параллельных прямых а и b, и секущей с. Значит, сумма этих углов должна равняться 180 градусам по свойству параллельных прямых. Но угол 1 известен, так как а перпендикулярна с, то угол равен 90 по определению перпендикулярности.
Найдем угол 2.
$$<1+<2=180$$
$$<1=90$$
$$<2=180-<1$$
$$<2=180-90=90$$
Значит, прямая с перпендикулярна прямой b по определению перпендикулярности.
Этим следствием можно пользоваться так же, как и остальными, но и забывать о том, что оно не является следствием в полном смысле этого слова не нужно.

Что мы узнали?
Мы поговорили об истории появления формулировки аксиомы параллельных прямых, узнали автора аксиомы и привели три следствия из нее, доказав третье.
Тест по теме
- /5Вопрос 1 из 5
Как звучит пятый постулат аксиома Евклида?