Образовака📐 Геометрия7 классПараллельные прямые

Признаки параллельных прямых

4.1

Средняя оценка: 4.1

Всего получено оценок: 288.

Параллельность – очень полезное свойство в геометрии. В реальной жизни параллельные стороны позволяют создавать красивые, симметричные вещи, приятные любому глазу, поэтому геометрия всегда нуждалась в способах эту параллельность проверить. О признаках параллельности прямых мы и поговорим в этой статье.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Определение для параллельности

Выделим определения, которые необходимо знать для доказательства признаков параллельности двух прямых.

Прямые называют параллельными, если они не имеют точек пересечения и лежат в одной плоскости. Кроме того, в решениях обычно параллельные прямые идут в связке с секущей прямой.

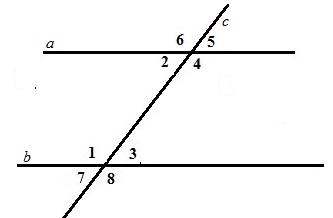
Рис. 1. Углы при параллельны прямых и секущей.

Секущей прямой называется прямая, которая пересекает обе параллельные прямые. В этом случае образуются накрест лежащие, соответственные и односторонние углы. Накрест лежащими будут пары углов 1 и 4; 2 и 3; 8 и 6; 7 и 5. Соответственными будут 7 и 2; 1 и 6; 8 и 4; 3 и 5.

Односторонними 1 и 2; 7 и 6; 8 и 5; 3 и 4.

При правильном оформлении пишется: «Накрест лежащие углы при двух параллельных прямых а и b и секущей с», потому что для двух параллельных прямых может существовать бесконечное множество секущих, поэтому необходимо указывать, какую именно секущую, вы имеете в виду.

Также для доказательства понадобится теорема о внешнем угле треугольника, которая гласит, что внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.

Признаки

Все признаки параллельности прямых завязаны на знание свойств углов и теоремы о внешнем угле треугольника.

Признак 1

Две прямые параллельны, если накрест лежащие углы равны.

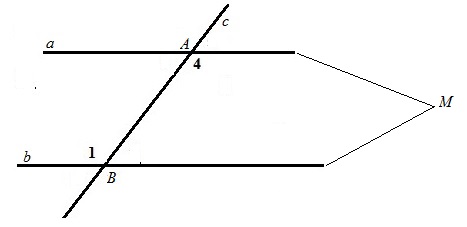
Рассмотрим две прямые а и b с секущей с. Накрест лежащие углы 1 и 4 равны. Предположим, что прямые не параллельны. Значит прямые пересекаются и должна быть точка пересечения М. Тогда образуется треугольник АВМ с внешним углом 1. Внешний угол при вершине В должен быть равен сумме углов 4 и АМВ, как несмежных с ним, по теореме о внешнем угле в треугольнике. Но тогда получится, что угол 1 больше угла 4, а это противоречит условию задачи, значит, точки М не существует, прямые не пересекаются, то есть параллельны.

Признак 2

Две прямые параллельны, если соответственные углы при секущей равны.

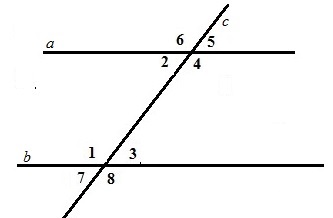
Рассмотрим две прямые а и b с секущей с. Соответственные углы 7 и 2 равны. Обратим внимание на угол 3. Он является вертикальным для угла 7. Значит, углы 7 и 3 равны. Значит, углы 3 и 2 также равны, так как <7=<2 и <7=<3. А угол 3 и угол 2 являются накрест лежащими. Следовательно, прямые параллельны, что и требовалось доказать.

Признак 3

Две прямые параллельны, если сумма односторонних углов равна 180 градусам.

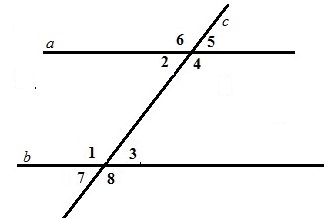
Рассмотрим две прямые а и b с секущей с. Сумма односторонних углов 1 и 2 равна 180 градусов. Обратим внимание на углы 1 и 7. Они являются смежными. То есть:

$$<1+<7=180$$

$$<1+<2=180$$

Вычтем из первого выражения второе:

$$(<1+<7)-(<1+<2)=180-180$$

$$(<1+<7)-(<1+<2)=0$$

$$<1+<7-<1-<2=0$$

$$<7-<2=0$$

$<7=<2$ – а они являются соответственными. Значит, прямые параллельны.

Что мы узнали?

Мы в подробностях разобрали, какие углы получаются при пересечении параллельных прямых третьей прямой, выделили и подробно расписали доказательство трех признаков параллельности прямых.