Площади подобных треугольников


Средняя оценка: 4.8
Всего получено оценок: 239.
Средняя оценка: 4.8
Всего получено оценок: 239.
Подобные треугольники – это следующий шаг в изучении треугольников после равенства. Нужно в полной мере понимать возможности подобия треугольников, чтобы правильно использовать все свойства в решении задач. Разберемся в отличиях равенства, подобия и равновеличия, а также поговорим о свойствах сторон и определении площадей подобных треугольников.
Подобные треугольники
Подобными треугольниками называют треугольники, соответственные стороны которых пропорциональны, а углы равны. Равные треугольники также являются подобными с коэффициентом подобия равным 1.
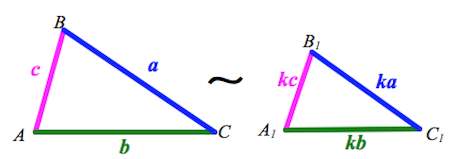
Коэффициент пропорциональности (подобия) – это отношение длин сторон одного треугольника к соответствующим длинам сторон другого треугольника. Важно при подсчете коэффициента строго соблюдать какая сторона к какой относится.
Например, если вы начали расчет делением сторон большего треугольника на стороны меньшего, то стоит придерживаться такого подхода и далее.
Признаки подобия
Признаки подобия в чем-то похожи на признаки равенства треугольников. Всего их тр:
- По двум углам. Если два угла одного треугольника равны соответствующим углам другого треугольника, то такие треугольники подобны.
- По трем сторонам. Если три стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника, то такие треугольники подобны.
- По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.

Свойства подобных треугольников
- Стороны подобных треугольников пропорциональны и относятся друг к другу в отношении, равном коэффициенту подобия.
- Углы подобных треугольников равны.
- Площади подобных треугольников относятся друг к другу в отношении, равном квадрату коэффициента подобия.
Остановимся подробнее на последнем свойстве. Почему все стороны соотносятся ,как коэффициент в первой степени, а площади в квадрате? Потому что площадь это половина произведения основания на высоту.
Пропорциональны друг другу не только стороны, но и характерные отрезки: медианы, высоты, биссектрисы.
Получается, что обе части произведения площади пропорциональны, но в произведении участвуют как высота, так и основание. Значит коэффициент пропорциональности должен быть возведен в квадрат.
$$S_1={1\over{2}}*h_1*a_1$$
$$S_2={1\over{2}}*h_2*a_2$$
$${S_1\over{S_2}}={{h_1*a_1}\over{h_2*a_2}}$$
$${S_1\over{S_2}}={h_1\over{h_2}} *{a_1\over{a_2}}$$
$${S_1\over{S_2}}=k *k$$
$${S_1\over{S_2}}=k ^2$$
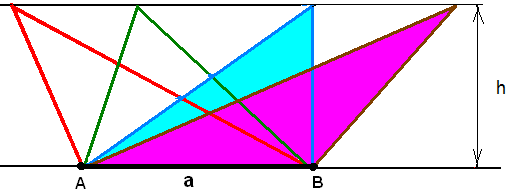
Нужно четко различать понятие подобных и равновеликих треугольников. Подобные треугольники имеют коэффициент подобия, в соответствие с которым соотносятся стороны треугольника. А равновеликие треугольники могут, как угодно разнится по значениям сторон, важно лишь, чтобы площади треугольников были равны.

Что мы узнали?
Мы узнали, что такое подобные треугольники, поговорили об их свойствах. Поговорили об отношении площадей подобных треугольников и вывели это отношение на практике для лучшего запоминания формулы.
Тест по теме
- /5Вопрос 1 из 5
Подобные треугольники – это …