Образовака💯 Математика4 классЧисла от 1 до 1000

Равные треугольники

4.5

Средняя оценка: 4.5

Всего получено оценок: 446.

Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Определение

Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.

Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.

Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$

Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.

Признаки равенства

Выделяют три признака равенства треугольников:

1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.

2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.

3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.

Кроме того, стоит выделить некоторые свойства:

Сумма двух внутренних углов треугольника будет всегда меньше 180⁰.
Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Алгоритм доказательства равенства фигур

Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
На рисунке отметить, все необходимые данные в условии задания.
Проверить есть ли у двух треугольников общая сторона либо угол.
Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
При необходимости, можно сделать дополнительное построение.

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Пример

Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.

Решение:
Стоит обратить внимание на рисунок

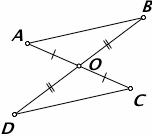
В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.

Что мы узнали?

Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.