Вращательное движение

4.2

Средняя оценка: 4.2

Всего получено оценок: 156.

4.2

Средняя оценка: 4.2

Всего получено оценок: 156.

Одним из наиболее часто встречающихся криволинейных движений является вращательное движение. Рассмотрим особенности такого движения подробнее.

Вращательное движение

Абсолютно твердое тело

Для описания вращательного движения нельзя использовать понятие материальной точки, поскольку оно предполагает, что все точки тела движутся одинаково.

При вращательном движении ситуация иная. Различные точки тела всегда движутся по-разному. Поэтому для вращательного движения вместо понятия «материальной точки» используется понятие «абсолютно твердого тела».

Равномерное вращение абсолютно твердого тела

Вращением абсолютно твердого тела называют такое движение материальных точек, составляющих тело, при котором траектории движения точек представляют собой окружности с центрами, лежащими на одной прямой. Эта прямая называется «осью вращения», и как правило (но необязательно), проходит через само тело. При этом плоскости, в которых лежат траектории, параллельны между собой и перпендикулярны оси вращения. Примерами вращательного движения являются движение колес автомобиля, движение шестерен в механических часах, движение роторов электрических двигателей.

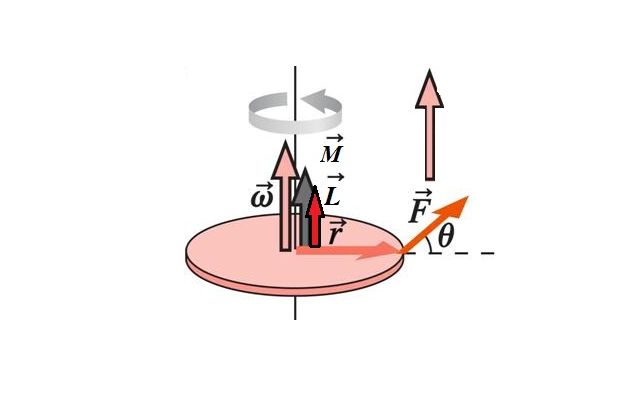
При равномерном вращательном движении все точки тела поворачиваются на один и тот же угол за одно и то же время, поэтому скорость вращения измеряется в радианах в секунду:

$$\omega ={Δ\phi \over Δt},$$

где:

• $Δ\phi$ – угол поворота, радиан.
• $Δt$ – время, за которое поворот совершается, секунд.

Иногда известна не угловая скорость, а время одного оборота (период) $T$ (секунд) или частота, с которой происходит вращение $\nu$ (оборотов в секунду). Эти величины связаны соотношением

$$\omega = {2\pi\over T}=2\pi\nu$$

В отличие от поступательного движения, точки тела при вращении имеют различные мгновенные скорости. Эту особенность вращения легко объяснить, если учесть, что длина траектории зависит от ее радиуса. Если радиус траектории $R$, то длина траектории будет равна $2\pi R$, и мгновенная линейная скорость будет связана с угловой скоростью, периодом и частотой вращения соотношением

$$v=\omega R={2\pi R\over T}=2\pi\nu R$$

Центростремительное ускорение

Хотя при равномерном вращении модуль скорости каждой точки постоянен, его направление постоянно изменяется. Следовательно, вращение – это движение с ускорением, которое называется центростремительным. Такое название подчеркивает, что ускорение меняет не значение, а направление вектора скорости, и направлено оно всегда к центру вращения.

Модуль центростремительного ускорения равен:

$$a_ц=\omega^2R={4\pi ^2 R\over T^2}={4\pi ^2\nu^2 R}$$

Что мы узнали?

Абсолютно твердое тело – это система материальных точек, взаимное расположение которых неизменно. Вращательное движение абсолютно твердого тела – это такое движение его точек, при которых траектории движения представляют окружности с центрами, лежащими на одной прямой – оси вращения.

Тест по теме

Доска почёта

Чтобы попасть сюда - пройдите тест.