Биссектриса треугольника

4.2

Средняя оценка: 4.2

Всего получено оценок: 390.

Биссектриса является одним из основных понятий курса геометрии. Особая роль отводится понятию биссектрисы угла треугольника. В статье мы познакомимся с понятием биссектрисы, с ее свойствами, а затем решим задачу для закрепления материала.

Определения понятия биссектрисы

Биссектрисой треугольника называется отрезок, который делит угол треугольника на два равных угла. К примеру, если угол треугольника 120⁰, то проведя биссектрису, мы построим два угла по 60⁰.

А так как в треугольнике имеется три угла, то можно провести три биссектрисы. Все они имеют одну точку пресечения. Эта точка является центром окружности, вписанной в треугольник. По-другому эту точку пересечений называют инцентром треугольника.

При пересечении двух биссектрис внутреннего и внешнего угла, получается угол 90⁰. Внешний угол в треугольнике угол, смежный с внутренним углом треугольника.

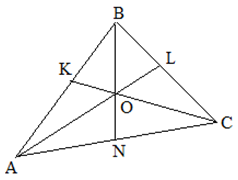
Рис. 1. Треугольник, в котором проведены 3 биссектрисы

Биссектриса делит противоположную сторону на два отрезки, которые имеют связь со сторонами:

$${CL\over{LB}} = {AC\over{AB}}$$

Точки биссектрисы равноудаленные от сторон угла, это значит, что они находятся на одинаковом расстоянии от сторон угла. То есть, если из любой точки биссектрисы опустить перпендикуляры на каждую из сторон угла треугольника, то эти перпендикуляры будут равны..

Если с одной вершины провести медиану, биссектрису и высоту, то медиана будет самым длинным отрезком, а высота самым коротким.

Некоторые свойства биссектрисы

В определенных видах треугольников, биссектриса имеет особые свойства. В первую очередь это относится к равнобедренному треугольнику. Эта фигура имеет две одинаковые боковые стороны, а третья называется основанием.

Если из вершины угла равнобедренного треугольника провести биссектрису к основанию, то она будет иметь свойства одновременно и высоты и медианы. Соответственно, длина биссектрисы совпадает с длиной медианы и высоты.

Определения:

Высота – перпендикуляр, опущенный из вершины треугольника к противоположной стороне..
Медиана – отрезок, который соединяет вершину треугольника и середину противоположной стороны.

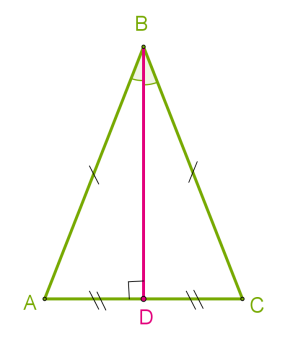
Рис. 2. Биссектриса в равнобедренном треугольнике

Это касается и равностороннего треугольника, то есть треугольника, в котором все три стороны равны.

Пример задания

В треугольнике ABC: BR биссектриса, причем AB = 6 см, BC = 4 см, а RC = 2 см. Вычесть длину третей стороны.

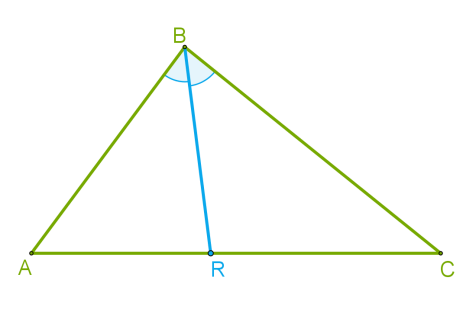
Решение:

Биссектриса делит сторону треугольника в определенной пропорции. Воспользуемся этой пропорцией и выразим AR. После найдем длину третьей стороны как сумму отрезков, на которые эту сторону поделила биссектриса.

${AB\over{BC}} = {AR\over{RC}}$
$RC={6\over{4}}*2=3 см$

Тогда весь отрезок AC = RC+ AR

AC = 3+2=5 см.

В равнобедренном треугольнике биссектриса, проведенная к основанию, делит треугольник на два равных прямоугольных треугольника.

Что мы узнали?

Изучив тему биссектрисы, мы узнали, что она делит угол на два равных угла. А если ее провести в равнобедренном либо равностороннем треугольнике к основанию, то она будет иметь свойства и медианы и высоты одновременно.