Образовака📐 Геометрия7 классСоотношения между сторонами и углами треугольника

Биссектриса равнобедренного треугольника

4.6

Средняя оценка: 4.6

Всего получено оценок: 230.

Биссектриса равнобедренного треугольника обладает особенным свойством, которое определяет стиль решения задач на нахождение элементов равнобедренного треугольника. Чтобы лучше понять смысл решения подобных задач, поговорим о биссектрисе равнобедренного треугольника.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Определения

Равнобедренный треугольник – это треугольник, две стороны которого равны между собой. Третья сторона зовется основанием, углы при основании равны.

Биссектриса треугольника – это отрезок, который делить угол треугольника на две равные части. Каждая точка биссектрисы равноудалена от каждой из сторон треугольника, т.е. если из любой точки биссектрисы опустить перпендикуляры на каждую из сторон угла, то эти перпендикуляры окажутся равны между собой. Точка пересечения биссектрис является центром вписанной в треугольник окружности и зовется инцентром треугольника.

Биссектриса равнобедренного треугольника

Равнобедренный треугольник уникален равенством двух сторон и двух углов. Именно этим обеспечивается основное свойство биссектрисы равнобедренного треугольника: в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с высотой и медианой.

В равнобедренном треугольнике только биссектриса, проведенная к основанию, совпадает с высотой и медианой. Две другие биссектрисы будут отличатся от соответствующих медиан и высот, проведенным к этим же сторонам. Это стоит запомнить раз и навсегда, чтобы не допускать нелепых ошибок.

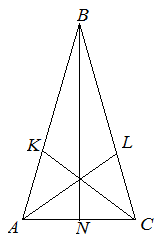
Рис. 2. Биссектрисы в равнобедренном треугольнике

При решении задач, нужно понимать, что это свойство можно применять не только в равнобедренном, но и в равностороннем треугольнике.

Ведь, если выбрать любую из сторон равностороннего треугольника и принять ее за основание, то две другие стороны будут равны, а, значит, равносторонний треугольник может считаться равнобедренным треугольником, у которого любая сторона может выступать в роли основания.

А раз любую сторону можно принимать за основание, то и каждая биссектриса будет совпадать с каждой соответствующей медианой и высотой. Ведь каждая биссектриса будет проведена к стороне, которую можно считать основанием.

Именно на этом свойстве основано равенство двух треугольников, которые получаются в равнобедренном треугольнике в результате проведения биссектрисы. Ведь в таких треугольниках одна сторона, та самая биссектриса, будет общей.

Рис. 3. Равнобедренный тупоугольный треугольник

Биссектриса совпадает с высотой, а, значит, два малых треугольника будут прямоугольными, а биссектриса дает два равных угла. То есть, два треугольника будут равны по катету и прилежащему острому углу, что соответствует одному из признаков равенства прямоугольных треугольников.

Использование двух малых треугольников часто встречается на практике. Например, если известны основание треугольника и его боковая сторона, а нужно найти биссектрису, сделать это можно гораздо проще, нежели в других треугольниках.

Биссектриса совпадает с медианой и высотой, а, значит, станет катетом малого прямоугольного треугольника, тогда значение биссектрисы можно найти как значение катета через теорему Пифагора.

Что мы узнали?

Мы вспомнили, что такое равнобедренный треугольник. Поговорили о свойствах биссектрисы равнобедренного треугольника, отдельно выделили свойства биссектрис равностороннего треугольника. Отметили наиболее применяемый и простой способ нахождения биссектрисы равнобедренного треугольника.