Стороны равнобедренного треугольника


Средняя оценка: 4.1
Всего получено оценок: 272.
Средняя оценка: 4.1
Всего получено оценок: 272.
Стороны равнобедренного треугольника найти достаточно просто – нужно лишь выработать навык и научиться пользоваться теоремами об этой фигуре, которых не так много. Поговорим о каждой из сторон треугольника и способах определения отдельно.
Равнобедренный треугольник
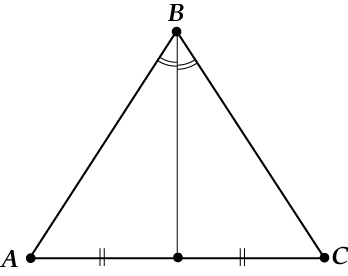
Равнобедренный треугольник – это треугольник, две стороны которого равны, а третья является основанием.

Только в равнобедренном треугольнике основание имеет реальное практическое применение. Для лучшего визуального восприятия фигуры стоит располагать чертеж так, чтобы основание располагалось внизу. Это не принципиальный вопрос и иногда решение вынуждает нас располагать фигуру иначе, но если есть возможность, то стоит поместить основание внизу фигуры.
Свойства равнобедренного треугольника
Свойств равнобедренного треугольника не так много. В решениях школьных задач даже старших классов используется всего 3 свойства:
- Боковые стороны треугольника равны.
- Биссектриса треугольника совпадает с медианой и высотой.
- Углы при основании равнобедренного треугольника равны.
Этих свойств вполне достаточно, чтобы использовать стиль решения неприменимый для любого другого треугольника.

Стороны равнобедренного треугольника
Равнобедренный треугольник отличается от остальных фигур тем, что достаточно двух показателей, из которых хотя бы один должен быть стороной, чтобы решить весь треугольник.
Например, если известна боковая сторона и угол при основании, то можно провести медиану, она совпадет с биссектрисой и высотой, разбив треугольник на два малых равных между собой прямоугольных треугольников.
В этих треугольниках известна гипотенуза, которая является одновременной боковой стороной равнобедренного треугольника и угол при ней. Значит, через тригонометрическую функцию известного угла, т.е. через синус или косинус, можно найти каждый из катетов.
Один из катетов является биссектрисой, высотой и медианой. Второй – половиной основания. Почему половиной? Потому что часть отрезка, которая является катетом, отсекается от основания отрезком, который можно считать медианой. А медиана это отрезок, который соединяет вершину с серединой противоположной стороны.
Тригонометрическую функцию известного угла можно определить по таблицам Брадиса. В этих таблицах рассчитаны значения для всех существующих целых и промежуточных углов.
Как найти оставшийся третий угол? С помощью все тех же тригонометрических функций. В малом прямоугольном треугольнике известен один угол, который является при этом углом при основании равнобедренного треугольника. В прямоугольном треугольнике сумма острых углов равняется 90 градусам, то есть вычитаем известное значение из 90 и получаем половину угла напротив основания.
Почему половину? Потому что высота, которая образовала два равных прямоугольных треугольника, является одновременно и биссектрисой. Поэтому полученное значение нужно умножить на два и получить результат.
Равнобедренный треугольник нельзя решить, если:
- Известны только 2 боковые стороны.
- Известны только углы.
- Известно только основание.
- Известна только величина любого из характеризующих отрезков: высота, медиана, биссектриса и т.д.
Во всех остальных случаях треугольник можно решить. Зачем знать варианты, когда решение точно невозможно? Чтобы не попасть в ловушку нерешаемых задач. Такие редко, но встречаются. Предоставляя их к решению, составители проверяют уровень знаний учеников о фигуре.

Что мы узнали?
Мы поговорили о том, что такое равнобедренный треугольник, выделили основные его свойства и поговорили о формулах сторон равнобедренного треугольника.
Тест по теме
- /10Вопрос 1 из 10
Сколько сторон у равнобедренного треугольника?