Образовака💯 Математика5 классНатуральные числа

Цифры

4.6

Средняя оценка: 4.6

Всего получено оценок: 569.

Под цифрами в математике понимают упорядоченную систему символов для записи чисел. Это своего рода шифр, который объединяет математику всего мира. Именно поэтому необходимо так важно разбираться в этой теме.

Характеристики понятия

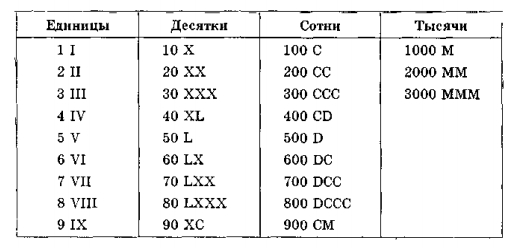
Раньше люди обозначали числа различными значками: одна вертикальная короткая линия изображала единицу, а две – двойку и так далее. Этот метод записи до сих пор можно увидеть в записи «римских цифр».

Однако для громоздких вычислений в математике римский метод записи неудобен. Поэтому в обиход вошли арабские цифры. Ими было удобно пользоваться для различных видов вычислений. При этом арабские цифры удобно использовать не только в математике, но и в программировании, что стало еще одной причиной повсеместного распространения именно этого вида записи.

На самом деле арабские цифры являются индийскими. Но арабские страны переняли множество культурных особенностей у Индии. К тому же, многие математические трактаты древности составлены именно арабами с применением индийской системы исчисления. Позже, во время перевода трудов по математике, переводчики не стали искать корни происхождения цифр и назвали их арабскими.

Рис. 1. Таблица соответствия римских и арабских цифр.

Значение

Существуют разные варианты записи чисел. В зависимости от количества первоначальных цифр. В привычной нам десятичной системе их 10: от 0 до 9. Существует двоичная система, которая используется всего две цифры: 0 и 1. Эта система распространена в программировании. Существует множество других систем, каждая из которых когда-то использовалась человечеством. Но наиболее удобной была признана десятеричная с использованием арабских цифр.

В 5 классе изучают однозначные и многозначные натуральные числа. Получается, что в первом случае берется только одна цифра, а во втором – несколько. Наименьшим однозначным простейшим числом является «1», а наибольшим – «9».

Цифры, входящие в состав многозначного числа занимают определенные позиции, которые относят к разрядам.

Если в числе отсутствует разряд, то вместо него будет записана цифра «0». К примеру, запись «90» означает, что здесь содержится 9 десятков и 0 единиц. При этом разряды перед значащей цифрой тоже есть, но их не пишут. То есть, можно было бы записать «090», просто это загромождает запись.

Формирование больших чисел

Легко запоминать и читать длинные числа поможет знание классов. К первому классу относят первые три разряда: единицы, десятки и сотни. Все вместе они называются единицами. Следующий класс это три разряда тысяч, затем три разряда сотен тысяч, потом миллионы и так далее.

Для удобства классификации используют небольшие пробелы. К примеру, число 23465787 записывают так: 23 465 787. Тут совокупность цифр 787 относят к первому классу, 465 – второму, 23 – третьему. Обычно название класса единиц не проговаривают, так же как не проговаривают и название нулевых разрядов.

Что мы узнали?

Из определения понятия «цифра», нам стало известно, что это специальный знак, который используется для обозначения чисел. В современной математике используются «арабские цифры». Этот способ записи оказался более удобным для счислений. Полученное многозначное число читают слева на право, называя число единиц каждого класса с последующим добавлением названия класса.