Образовака💯 Математика4 классЧисла, которые больше 1000

Диагональ прямоугольника

4.7

Средняя оценка: 4.7

Всего получено оценок: 173.

В школьном курсе математики одной из первых в изучении фигур является прямоугольник. Диагональ прямоугольника участвует в решении многих задач. Поэтому имеет смысл подробнее рассмотреть этот элемент фигуры.

Определение

Прямоугольник является четырехугольником с равными углами и попарно равными и параллельными противоположными сторонами.

Поэтому диагональ будет делить данную геометрическую фигуру на два прямоугольных треугольника. Получается, что значение этого отрезка можно будет найти через корень квадратный суммы квадратов соответствующих сторон прямоугольника (по теореме Пифагора).

Диагональ прямоугольника обозначают маленьким латинским символом d или двумя заглавными буквами, по названию вершин, которые соединяет диагональ.

Длина диагонали прямоугольника, вокруг которого описана окружность, равняется диаметру этой окружности.

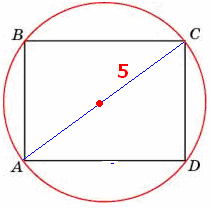
Рис. 1. Диагональ вписанного прямоугольника.

Это свойство может помочь в решении задач на нахождение сторон треугольника.

Характеристики понятия

Диагональ прямоугольника это отрезок, соединяющий вершины прямоугольника, находящиеся напротив друг друга. Рассматриваемый параметр можно найти, используя периметр основной геометрической фигуры, ее площадь или соотношение соответствующих сторон. Для этого используют формулу диагонали прямоугольника:

$d=\sqrt{a^2+b^2}$, где а и b – стороны прямоугольника.

Определение длины диагонали через свойства прямоугольника” url= — Рис. 2. Свойства прямоугольника

Значение

В математике различают свойства диагоналей прямоугольника. Так, эти отрезки пересекаются в одной точке, и точкой пересечения делятся пополам. В одном прямоугольнике диагонали будут равными.

На этом рисунке четко просматриваются углы, которые формируют диагонали.

Если диагонали параллелограмма равны, то эта геометрическая фигура является прямоугольником. Можно утверждать то же самое, когда сумма квадратов отрезков параллелограмма равна квадрату его диагонали (естественно речь идет о теореме Пифагора).

Что мы узнали?

Свойства диагонали прямоугольника используются для нахождения важных параметров этой фигуры. Решения задач, в которых требуется доказать наличие определенного типа четырехугольника нередко рассматривают диагонали параллелограмма. С помощью данных отрезков можно найти площадь фигуры, которой они принадлежат.