Образовака💯 Математика5 классУмножение и деление натуральных чисел

Площадь прямоугольника

4.4

Средняя оценка: 4.4

Всего получено оценок: 177.

Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из наиболее простых в изучении.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Понятия площади

Любая фигура имеет свою площадь, а вычисление площади отталкиваются от единичного квадрата, то есть от квадрата с длиной стороны в 1 мм, либо 1 см, 1 дм и так далее. Площадь такой фигуры равна $1*1 = 1мм^2$, либо $1см^2$ и т. д. Площадь, как правило, обозначается буквой S.

Площадь показывает размер части плоскости, которую занимает фигура, очерченная отрезками.

Прямоугольником называется четырехугольник, у которого все углы одинаковой градусной меры и равны по 90 градусов, а противоположные стороны попарно параллельны и равны.

Особое внимание нужно обращать на единицы измерения длины и ширины. Они должны совпадать. Если единицы не совпадают, их переводят. Как правило переводят большую единицу в меньшую, например, если длина дается в дм, а ширина в см, то дм переводят в см, а результат получится в $см^2$.

Формула площади прямоугольника

Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.

Рис. 1. Прямоугольник, разбитый на единичные квадраты

Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см². Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, поэтому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина. Таким образом, можно вывести формулу площади прямоугольника:

S = a · b, где a,b – ширина и длина фигуры.

К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см².

Расчет площади прямоугольника, с использованием его диагонали

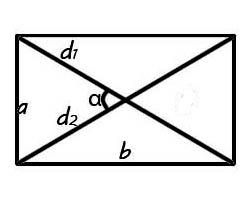
Для того, чтобы рассчитать площадь прямоугольника через диагональ необходимо применить формулу:

$$S = {1\over{2}} ⋅ d^2 ⋅ sin{α}$$

Если в задании дано значения угла между диагоналями, а также значение самой диагонали, то можно вычислить площадь прямоугольника по общей формуле произвольных выпуклых четырехугольников.

Диагональ – это отрезок, который соединяет противоположные точки фигуры. Диагонали прямоугольника равны, и точкой пересечения делятся пополам.

Рис. 2. Прямоугольник с начерченными диагоналями

Примеры

Для закрепления темы рассмотрим примеры заданий:

№1. Найти площадь огородного участка, такой формы как на рисунку.

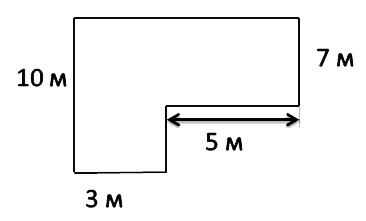
Решение:

Для того чтобы вычесть площадь, необходимо фигуру разбить на два прямоугольника. Один из них будет иметь размеры 10 м и 3 м, другой 5 м. и 7 м. Отдельно находим их площади:

$S_1 =3*10=30 м^2$;

$S_2=5*7=35 м^2$.

Далее необходимо найти их сумму:

$30+35=65 м^2$

Это и будет площадь огородного участка $S = 65 м^2$.

№2. Вычислить площадь прямоугольника, если его диагональ d=6 см. а угол между диагоналями α =30⁰.

Решение:

Значение $sin 30 ={1\over{2}} $,

$ S ={1\over{2}}⋅ d^2 ⋅ sinα$

$S ={1\over{2}} * 6^2 * {1\over{2}} =9 см^2$

Таким образом, $S=9 см^2$.

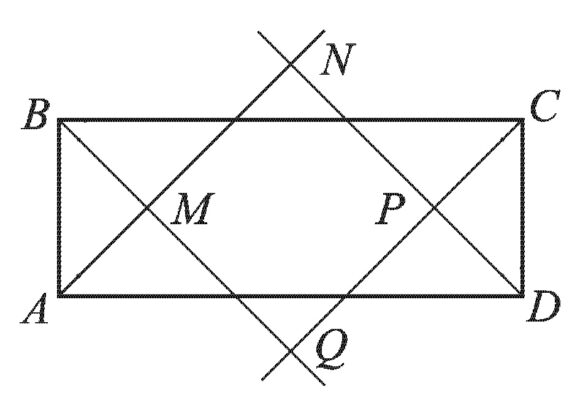
Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.

Диагонали не являются биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.

Что мы узнали?

Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также не стоит забывать, что если в задании разные единицы измерения сторон, то необходимо перевести их одну.