Объем прямоугольного параллелепипеда


Средняя оценка: 4.6
Всего получено оценок: 586.
Средняя оценка: 4.6
Всего получено оценок: 586.
В школьном курсе математики за 5 класс, ученики знакомятся с темой прямоугольного параллелепипеда. Это одна из первых фигур курса, имеющих объем. Именно об объеме и формуле его нахождения пойдет речь сегодня.
Определения
Прямоугольным параллелепипедом называется фигура, все грани которого – прямоугольники. Фигура имеет шесть граней. Грани, пресекаясь, образовывают ребра, их 12.
Прямоугольный параллелепипед имеет четыре боковые грани и две грани оснований. В жизни мы часто сталкиваемся с данной фигурой: шкаф, холодильник, коробка – все они имеют форму прямоугольного параллелепипеда.

Формула объема данной фигуры
Объем куба (фигуры, все грани которого квадраты) со стороной 1 единица называется 1 кубическая единица.

Если заложить такими кубиками дно фигуры (рис. 3), то в длину понадобится 4 куба, а в ширину 3.
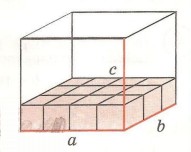
Таким образом, для заполнения основания необходимо:
3 х 4 =12 – так мы вычисляли площадь.
Чтобы заполнить всю фигуру и узнать объем, необходимо посчитать, сколько поместится в высоту таких слоев кубов, к примеру, если это будет 2, то объем составит:
3 х 4 х 2 = 24 кубов
Так, если учесть что длина основания фигуры 4 единицы, ширина – 3, высота – 2, то для того чтобы вычесть объем прямоугольного параллелепипеда необходимо найти произведение этих величин или измерений. Фигура, которая имеет три измерения, называется трехмерной либо объемной.
Для обозначения объема используют букву V.
Формула объема прямоугольного параллелепипеда имеет вид:
$$V = a · b · c$$
При необходимости все данные в задании необходимо перевести в одни единицы измерения.
Единицами измерения являются $мм^3, см^3, дм^3$ и так далее. Важно правильно читать: $1 м^3$ или кубический метр и так далее.
Английский иллюзионист провел 44 дня в стеклянном прямоугольном параллелепипеде, который был подвешен над рекой Темза. В его распоряжении была только вода, подушка, матрас и письменные принадлежности.
Задание: Вычислить объем фигуры, ширина которой 4 дм, длина 50 мм, а высота 10 см.
Решение: Для начала необходимо перевести все данные в одни единицы измерения.
$4 дм. = 40 см$;
$50 мм. = 5 см$.
$V = a • b • h$
$V = 40 • 5 • 10 = 200 см^3$
Таким образом, объем фигуры $V = 200 см^3$
Для измерения объема жидкости используют особую единицу измерения – литр (1 л).
Древние измерения жидкости, например кор = 220 л, бат = 22 л.
Измерения объема:
$$1 л = 1 000 см^3 = 1 дм^3$$
$$1 км^3 = 1000 000 000 м^3$$
$$1 м^3 = 1 000 дм^3 = 1 000 000 см^3$$
$$1 дм^3 = 1 000 см^3$$
$$1 см^3 = 1 000 мм^3$$

Что мы узнали?
Мы узнали, что для того, чтобы найти объем прямоугольного параллелепипеда необходимо умножить произведение длины и ширины основания на высоту фигуры. А также мы познакомились с единицами измерения объема.
Тест по теме
- /5Вопрос 1 из 5
Что находится основании прямоугольного параллелепипеда?