Образовака📐 Геометрия7 классТреугольники

Длина средней линии треугольника

4.3

Средняя оценка: 4.3

Всего получено оценок: 182.

Средняя линия треугольника интересный характеризующий отрезок, так как обладает несколькими свойствами, позволяющими найти простое решение для, казалось бы, сложной задачи. Поэтому рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Треугольник и его характеризующие отрезки

Треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от величин углов, треугольники делятся на:

Остроугольные
Тупоугольные
Прямоугольные

Основными характеризующими отрезками треугольника являются:

Медиана – отрезок, соединяющий вершину с серединой противоположной стороны.
Биссектриса – отрезок, проведенный из вершины угла к противоположной стороне и делящий угол пополам
Высота – перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.

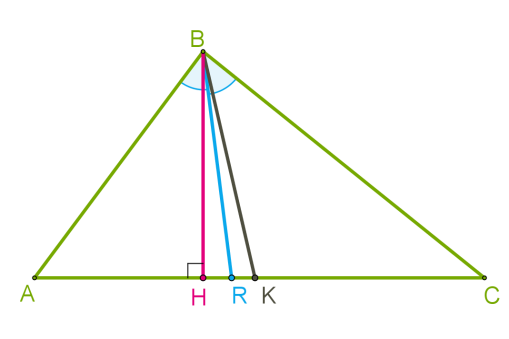
Рис. 2. Высота, медиана и биссектриса в треугольнике

Для каждого из характеризующих отрезков существует своя точка пересечения. При соединении трех точек пересечения медиан, биссектрис и высот получается золотое сечение треугольника.

Однако существует и ряд дополнительных характеризующих отрезков:

Серединный перпендикуляр – перпендикуляр восстановленный из середины стороны. Как правило серединный перпендикуляр продлевается до пересечения с другой стороной.
Средняя линия – отрезок, соединяющий середины смежных сторон.
Радиус вписанной окружности. Вписанная окружность – окружность, которая касается каждой из сторон треугольника. Центр вписанной окружности – точка пересечения биссектрис треугольника
Радиус описанной окружности. Описанная окружность – окружность, содержащая в себе все вершины треугольника. Центр описанной окружности – точка пересечения серединных перпендикуляров треугольника.

Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е. сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо – любая пара сторон в треугольнике является смежной.

Свойства средней линии

Свойств средней линии не так много, но все они имеют значение при решении задач. Дело в том, что задач на нахождение длины средней линии мало, а потому некоторые из них способны построить ученика в ступор при всей своей простоте.

Поэтому приведем и обсудим все свойства средней линии треугольника:

Средняя линия треугольника равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно. Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника.
Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в предыдущем свойстве.
Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5

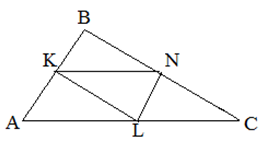
Собственно формула длины средней линии вытекает из второго свойства:

$m=1\over{2}*a$- где m – средняя линия, а – сторона противоположная средней линии.

Что мы узнали?

Мы поговорили о второстепенных характеризующих отрезках, выделив среднюю линию. Привели свойства средних линий и поговорили об особенностях формулировки этих свойств. Рассказали, как выводится формула длины средней линии треугольника и как средняя линия разбивает треугольник. Все эти свойства используются при решении треугольников.