Средняя линия прямоугольного треугольника


Средняя оценка: 4.2
Всего получено оценок: 111.
Средняя оценка: 4.2
Всего получено оценок: 111.
Прямоугольный треугольник стоит особняком от остальных треугольников. Прямой угол делает возможным применение других признаков равенства и подобия. Для углов в прямоугольном треугольнике можно без дополнительных построений использовать геометрические тождества, а любую из сторон можно найти по теореме Пифагора. Но среднюю линию прямоугольного треугольника определить трудно просто потому, что она редко упоминается в задачах, из-за чего мало кто может себе её визуально представить.
Что такое средняя линия прямоугольного треугольника?
Средняя линия – это отрезок, соединяющий середины сторон в треугольнике. В любом треугольнике можно провести три средних линии. При этом этот отрезок будет равен половине основания – это и считается формулой средней линии прямоугольного треугольника. Основанием считается сторона, с которой средняя линия не пересекается.
Средняя линия в треугольнике отсекает треугольник, подобный большому треугольнику, при этом площадь малого треугольника будет равна ¼ от площади большого, а коэффициент подобия будет равняться ½
Если в треугольнике провести все 3 средних линии, то образуется 4 равных между собой треугольника, которые при этом подобны большому треугольнику с теми же отношениями.
Причем, если средняя линия проводится в прямоугольном треугольнике, то каждый из четырех получившихся треугольников будет являться прямоугольным.
Все эти свойства можно использовать в ряде задач, что позволяет создавать интересные уникальные решения и доказательства.
Задача 1
В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. При этом MN=NP=2.
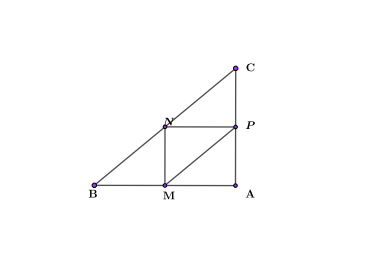
В центре треугольника средними линиями образован малый прямоугольный треугольник, катеты которого известны. Тогда его площадь равна: $S={1\over{2}}*MN*NP={1\over{2}}*2*2=2$.
Так как все 4 малых треугольника равны, то площадь большого будет равна: $S=4*2=8$
Задача 2
В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что диагональ MP равна 5, а синус угла между диагоналями равен 0,48. Найти площадь большого прямоугольного треугольника.
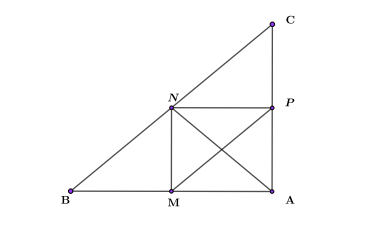
Рис. 2. Рисунок к задаче
В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP = 5, значит и вторая диагональ AN равна тоже 5.
Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.
$$S=5*5*0,48=12$$
В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольника, нужно умножить площадь прямоугольника на 2.
$S=12*2=24$ – ответ получен.
Задача 3
В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. Найти площадь прямоугольника MNPA, если известно, что площадь АВС равна 36.
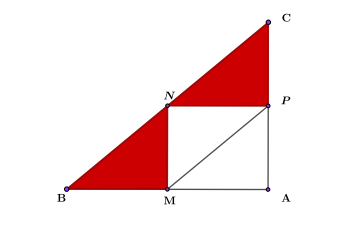
Аналогично с предыдущей задачей, можно вывести утверждение, что площадь треугольника равна двум площадям малого прямоугольника. Подставим в выражение цифры и выразим неизвестное. Площадь треугольника обозначим за S, прямоугольника s.
$$S=2s$$
$$s={S\over2}={36\over2}=18$$

Что мы узнали?
Мы узнали, что такое средняя линия, поговорили о свойствах средней линии и выделили особенности средней линии в прямоугольном треугольнике. Также мы закрепили пройденный материал, подробно изучив алгоритм решения задач на заданную тему.
Тест по теме
- /5Вопрос 1 из 5
Сколько малых треугольников образуется, если провести в треугольнике 3 средние линии?