Образовака📐 Геометрия7 классТреугольники

Неравенство треугольника

4.3

Средняя оценка: 4.3

Всего получено оценок: 591.

Любая фигура имеет некие рамки, пропорции длин сторон. В реальной жизни они помогают определить, можно ли изготовить треугольное основание определенных пропорций, насколько возможно создать линзу той или иной формы или может ли удержаться табуретка на треугольном, квадратном или любом другом основании. В теоретической геометрии пропорции, как правило, применяют для решения задач на доказательство или для определения правильности условия задачи.

Теорема о неравенстве треугольника

Именно с этой теоремы должно начинаться любое решение задачи. Но, как правило, это действие опускают. Считается, что составитель задач не может предложить условие с несуществующим треугольником.

Теорема о неравенстве сторон треугольника гласит, что каждая сторона треугольника всегда меньше или равна сумме двух других его сторон.

По факту, любая сторона треугольника всегда меньше суммы двух других его сторон. Равенство возможно, только если все три вершины треугольника лежат на одной линии. Можно ли считать такую фигуру треугольником – вопрос философов, а не математиков. Поэтому в формулировке ставится знак больше или равно.

Доказать это определение можно двумя способами: через аксиому Евклида или через высоту треугольника. Последний способ более логичен, тогда как второй – короче. Какой выбрать – решает доказывающий.

Доказательство через аксиому

Существует аксиома, которая говорит, что для трех точек А, В, С не лежащих на одной прямой справедливо утверждение: АВ< ВС+АС.

Эти точки можно принять за вершины треугольника, тогда расстояния между точками это стороны треугольника.

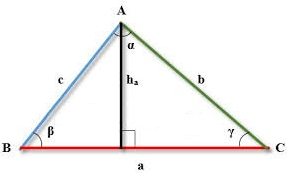
В произвольном треугольнике АВС проведем высоту АН. Высота разобьет произвольный треугольник на два прямоугольных. Тогда для каждого из прямоугольных треугольников в виде неравенств запишем, что катет всегда меньше гипотенузы.

Гипотенуза всегда больше катета потому, что в треугольнике действует отношение сторон и углов. Поэтому напротив наибольшего угла всегда находится наибольшая сторона. А в треугольнике наибольшим углом всегда является угол в 90 градусов.

ВН<АВ и НС<АС

Сложим два неравенства. Для этого нужно сложить правые части неравенств и левые с сохранением знака.

Например:

6<8

1<5

6+1<8+5

7<13, как видно неравенство все еще верно. Теперь проделаем ту же операцию с соотношением сторон в треугольнике:

ВН+НС<АВ+АС

ВН+НС=ВС

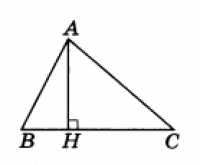
Значит, ВС<АВ+АС, то есть сторона меньше суммы двух других сторон, что и требовалось доказать. Высоту можно провести к любой стороне и повторить аналогичное доказательство. Как видно, все просто и ясно. Самое трудное: это разобраться в сложении неравенств.

Что мы узнали?

Мы узнали о теореме неравенства треугольников. Доказали ее различными способами, а также поговорили о том, для чего в мире нужны понятия пропорций в фигурах.