Образовака📐 Геометрия7 классТреугольники

Тупоугольный треугольник

4.6

Средняя оценка: 4.6

Всего получено оценок: 162.

Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник непривычным для восприятия. Это зачастую приводит в недоумение, поэтому стоит рассмотреть различные варианты решения задач на нахождение параметров тупоугольного треугольника.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики - более 33 лет.

Определения

Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном, это обычный треугольник и подход к решению таких фигур ничем не отличается.

Тупоугольный треугольник url= — Рис. 1. Тупоугольный треугольник.

В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.

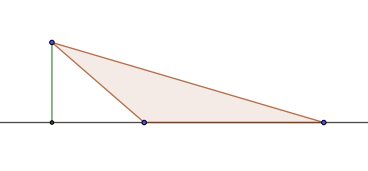
Рис. 2. Высота в тупоугольном треугольнике.

Только в тупоугольном треугольнике высота может лежать за пределами треугольника.

Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.

Пример решения задачи

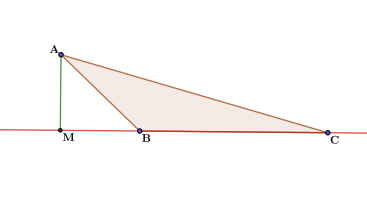
В тупоугольном треугольнике АВС известно, что косинус тупого угла равен $-2/\sqrt{13}$. Сторона АС находится напротив тупого угла, $АВ=\sqrt{13}$, ВС=2. Необходимо найти внешнюю высоту треугольника АМ.

Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.

Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.

Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно – как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.

$$sin(ABC)=\sqrt{1-cos^2(ABC)}=\sqrt{13-4 \over13}=\sqrt{9 \over13}={3\over\sqrt{13}}$$

Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.

$$S={1\over2}*AM*BC$$

$$S={1\over2}*AB*BC sin(ABC)$$

$${1\over2}*AM*BC={1\over2}*AB*BC*sin(ABC)$$

$$AM*ВС=AB*BC*sin(ABC)$$

$$AM=AB*sin(ABC)$$

$$AM=\sqrt{13}*{3 \over \sqrt{13}}=3$$

Второй способ – это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем, через значение косинуса найти значение синуса того же угла. А синус – это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза – это сторона АВ прямоугольного треугольника.

$$cos(ABM)=cos(180-ABC)=-cos(ABC)$$

$$cos(ABM)=-cos(ABC)={2\over \sqrt{13}}$$

Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.

$$Sin(ABM)=\sqrt{1-cos(ABM)^2}=\sqrt{13-4\over13}=\sqrt{9\over13}={3\over\sqrt{13}}$$

$$Sin(ABM)=AM/AB$$

$$AM=AB*sin(ABM)=\sqrt{13}*{3\over\sqrt{13}}=3$$

Третий метод – это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.

$$АС=\sqrt{AB^2+BC^2-2AB*BC*cos(ABC)}=$$

$$\sqrt {\sqrt{13}^2+2^2-2*\sqrt{13}*{-2\over\sqrt{13}}}=$$

$$\sqrt{13+4+8}=\sqrt{25}=5$$ – по теореме косинусов.

$${АС\over{sin(ABC)}}={AB\over{sin(ACB)}}$$ – по теореме синусов.

Значение синуса угла АВС определим по основному тригонометрическому тождеству.

$$ Sin(ABC)=\sqrt{1-cos^2(ABC)}=\sqrt{13-{4\over{4}}}=\sqrt{9\over{13}}={3\over\sqrt{13}}$$

Выразим искомый синус угла АСВ.

$$Sin(ACB)=AB*{sin(ABC)\over{AC}}$$

$$Sin(ACB)=(\sqrt{13}*{{3\over\sqrt{13}}\over{5}})={3\over5}$$

Выразим из треугольника АМС и найденного значения синуса сторону АМ.

$$Sin(ACB)={AM\over AC}$$

$$AM=sin(ACB)*AC$$

$$AM={3\over5}*{5}=3$$

Ответы всех трех способов совпали, а, значит, задача решена верно.

Что мы узнали?

Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а также выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.