Образовака💯 Математика6 классРациональные числа

Координатная плоскость

4.4

Средняя оценка: 4.4

Всего получено оценок: 246.

Координатная плоскость – это основа многих достижений человечества. Системы навигации, оптические прицелы, радиолокаторы: все это основано на плоских системах координат. Поговорим подробнее о данной теме в рамках курса математики за 6 класс.

Виды координатных плоскостей.

Многие не знают, что существует два вида координатных плоскостей. Это декартова система координат и полярная система координат.

Первая это всем привычная координатная сетка с двумя координатными осями. Именно такие сетки наносят на оптические прицелы. В этой системе положение точки на плоскости определяется двумя значениями координат.

Существует и альтернатива: полярная система координат. В этой системе положение точки определяется значением координатной прямой и высотой подъема точки над этой прямой, которая задается углом.

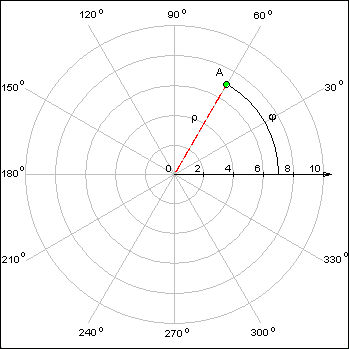
Этой системой пользовались древние мореплаватели задолго до изобретения более удобной декартовой системы. Но до сих пор полярная система координат имеет свои области применения.

Оси координатной плоскости

Осями координатной плоскости называют две перпендикулярные прямые, на которых отмечаются единичные отрезки начало координат. Началом координат и центром системы служит точка пересечения двух прямых.

Единичные отрезки осей могут не совпадать. Так за 1 по оси х может быть принять 1 см, а по оси у 10. Это вполне распространенная практика, которая применяется для более наглядного изображения рисунков, чертежей и графиков в координатной плоскости.

Оси координат традиционно обозначают х и у и называют соответственно осями абсцисс и ординат.

Рис. 3. Декартова система координат в пространстве.

В пространстве используется схожая система координат, только добавляется еще одна координатная ось z.

Определение координат

Для того чтобы определить координаты точки, опускают перпендикуляр на каждую из осей. Получаются два отрезка. Значение длин этих отрезков в заданных единицах длины и будет соответствовать координатам точки.

Соответственно, чтобы по координатам построить точку, нужно провести перпендикуляр из заданных точек на осях. В точке пересечения этих перпендикуляров и будет находиться искомая точка.

У координатной плоскости есть 4 четверти, в каждой из которых свои границы х и у. Будьте внимательны, координаты вполне могут быть отрицательными. Это всего лишь позволяет определить четверть координатной плоскости.

Что мы узнали?

Мы узнали, что такое координатная плоскость с координатами. Выделили элементы и квадраты координатной плоскости и поговорили о том, какие системы координат существуют. Рассказали о способе определения координат и построения точки по координатам. Выделили несколько нюансов построения координатной плоскости.